[이산수학] 수 체계 기호 조건 퍼셉트론
안녕하세요! 오늘도 이산수학에 대해서 배웠는데.. 그냥 수학분야가 아닌 인공지능이론이랑 결합되니까 정말 복잡해지네요 ㅎㅎ 근데 그만큼 또 재밌습니다!
자연수
- 사물을 셀 때나 순서를 매길 때 사용하는 수 1,2,3…
정수
- 자연수에 0과 음수를 더한것으로 -1,0,1 …
유리수
- 분자, 분모로 정수를 갖는 분수로 나타낼 수 있는 수
무리수
- Irrational number: 이치에 맞지 않는 수?
- ratio: 비율
- 즉 비율이 없는 수 또는 비율로 나타낼 수 없는 수
- e: 2.718 … pi: 3.41…
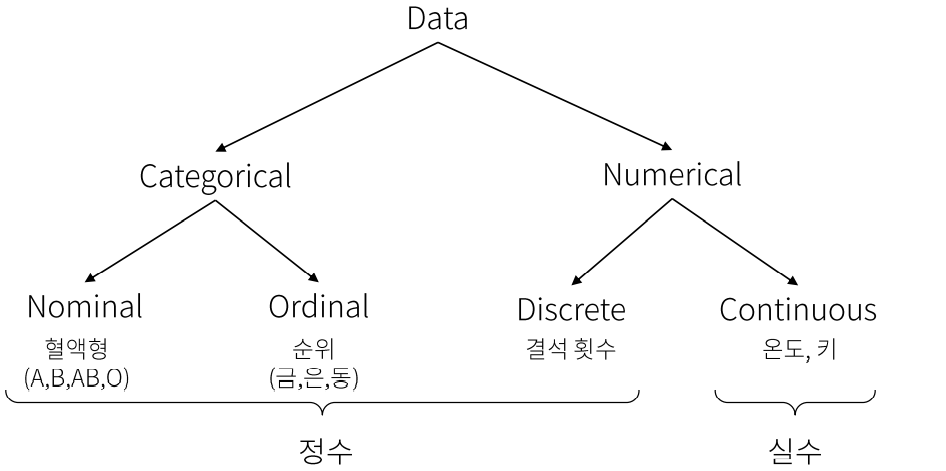
이건 우리가 다 아는 거죠? 이제 빅데이터나 인공지능에서 다루는 데이터들의 분류를 알아봅시다.
이렇게 나눌 수 있죠… 하지만 우리는 나중에 파이썬으로 분석을 해야해서 숫자로 전부 표현해야합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
data = {
'Name':['John', 'Sabre', 'Kim', 'Sato', 'Lee', 'Smith', 'David', 'Park'],
'Country':['USA', 'France', 'Korea', None, 'Korea', 'UK', 'USA', 'Korea'],
'Age':['31', 33, None, 40, 36, 55, np.nan, 35], # numerical인데 categorical처럼 인식될 수 있음
'Job':['Student', np.nan, 'Developer', 'Chef', 'Professor', 'CEO', 'Banker', 'Student'],
'Hand':['L', 'R', 'R', 'B', 'L', 'L', 'R', 'R'],
'Height':['T', 'S', 'M', 'S', 'T', 'S', 'S', 'T'],
'Capital':[48.35, 150.8, 99.0, 100.0, 182.3, 1101.65, 131.87, 65.8]
}
df_nan = pd.DataFrame(data)
df = df_nan.copy()
df
이렇게 데이터 프레임이 주어졌다면 age에는 문자로 입력된 것도 있고 주 손잡이도 문자로 되어있네요.
1
2
3
4
5
6
7
8
9
10
11
12
# Age -> Int16[+]로 변환하는 작업
df['Age'] =df['Age'].astype('Float32').astype('Int16')
df_enc = df.copy() #사본 카피
from sklearn.preprocessing import OrdinalEncoder #
# Hand 칼럼 ordinal [+]로 변환하는 작업
ord_enc = OrdinalEncoder()
ord_enc.fit(df[['Hand']])
ord_enc.transform(df[['Hand']])
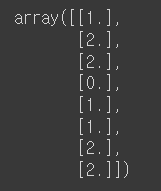
이렇게 age컬럼은 전부 정수로 바꿔주고 주손은 OrdinalEncoder()로 구분될 수 있는 숫자로 변환합니다.
이렇게요.. 하지만 나중에 어떤것이 어느 것을 가리킬지 모르니까
1
2
3
4
5
6
from sklearn.preprocessing import OneHotEncoder
# Hand 칼럼 onehot [+] - 해당 되는 곳에만 1표시
oh_enc= OneHotEncoder(sparse=False)
oh_enc.fit(df[["Hand"]])
oh_enc.transform(df[["Hand"]])
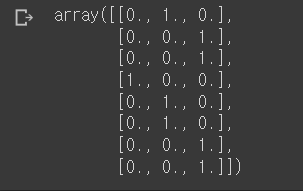
이렇게 원핫인코딩으로 해당되는 곳에만 1표시하도록 할 수도 있습니다.
이렇게요!
기호
시그마sigma
수열: 정의역이 자연수 전체 집합 n이고 공역이 실수 전체 집합 R인 함수
수열의 첫째 항부터 제 n항 까지의 합
프로덕트
합의 기호처럼 순서대로 모두 곱함
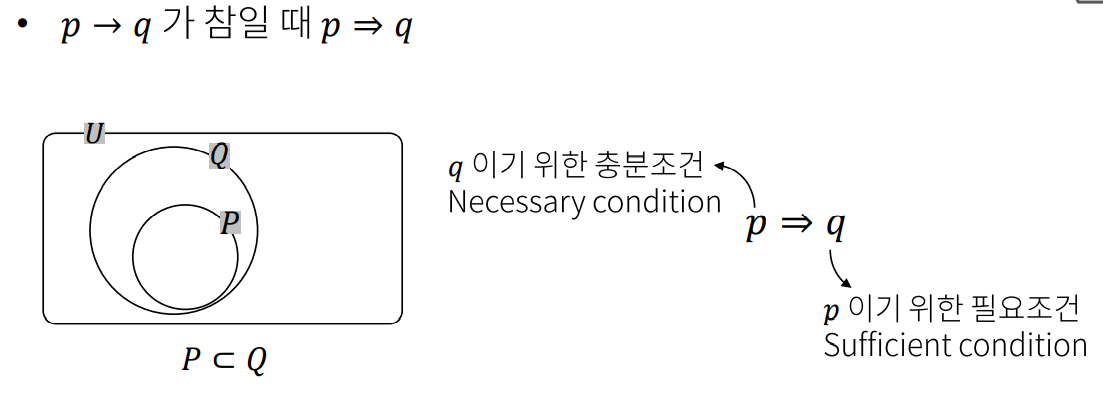
조건
필요조건과 충분조건
갑자기? 라는 생각이 들 수 있는데 필요조건과 충분조건은 나중에 함수를 미분하여 로스 펑션으로 함수의 로컬 미니멈값을 찾을 때 쓰입니다. 도함수f’(x) =0이 최소한의 조건, 즉 필요조건이 되는 것이죠.
퍼셉트론
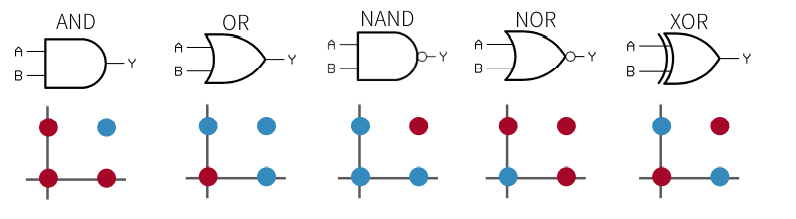
논리 게이트
부울 대수를 이용하여 회로를 설계할 때 회로의 기본 단위입니다. 퍼셉트론에서 이것을 활용하죠
퍼셉트론이란?
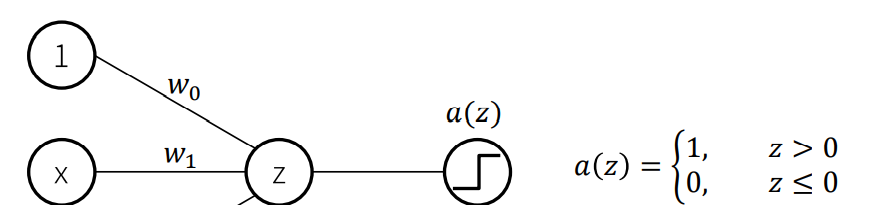
퍼셉트론(perceptron)은 인공신경망의 한 종류로서, 1957년에 코넬 항공 연구소(Cornell Aeronautical Lab)의 프랑크 로젠블라트 (Frank Rosenblatt)에 의해 고안되었습니다.
이런식의 변수와 상수의 가중치를 곱한 값을 더하고 그 값을 시그모이드 함수에 넣은 뒤 양수면1, 0과 같거나 음수면 0으로 분류를 할 수 있습니다.
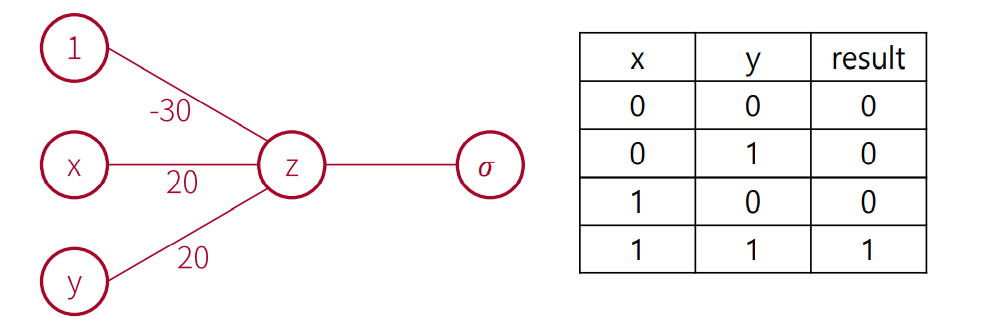
이처럼 AND 로직을 구현했습니다. x, y 둘다 1이어야(=and) 상수를 더했을 때 양수가 나오겠죠? 이런식입니다.
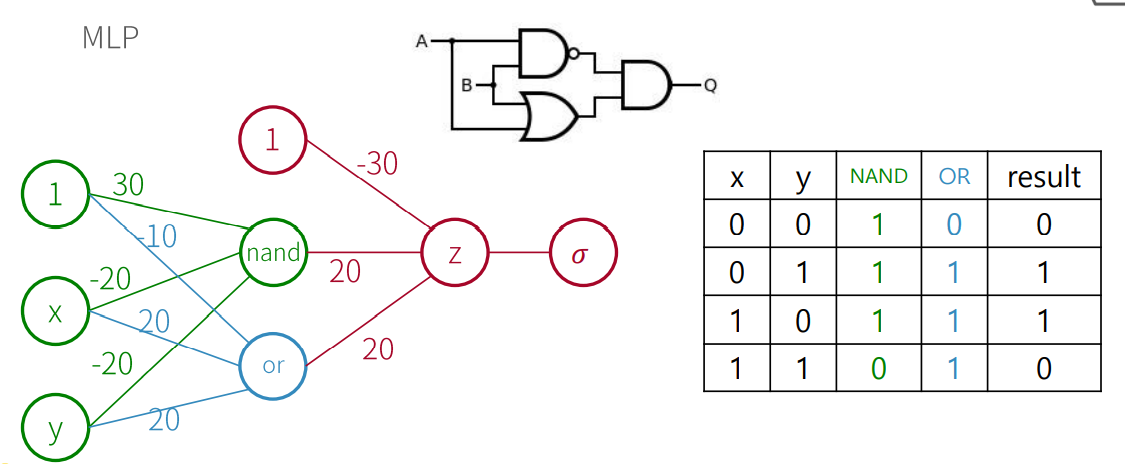 하이라이트입니다. xor논리인데요.. 이것 때문에 제1차 인공지능의 겨울이 왔었죠.. 이 복잡도가 너무 커진다는 이유였는데요, 논리는 간단합니다. 층을 하나 더 만들어서 한번 더 거쳐간 다음 합산을 하는 것이죠.
하이라이트입니다. xor논리인데요.. 이것 때문에 제1차 인공지능의 겨울이 왔었죠.. 이 복잡도가 너무 커진다는 이유였는데요, 논리는 간단합니다. 층을 하나 더 만들어서 한번 더 거쳐간 다음 합산을 하는 것이죠.
위처럼 NAND와 OR을 먼저 연산한 뒤 그 값들을 다시 AND로 연결하면 xor논리값이 나옵니다.
이번 시간에는 여기까지 하겠습니다!
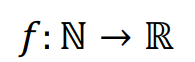
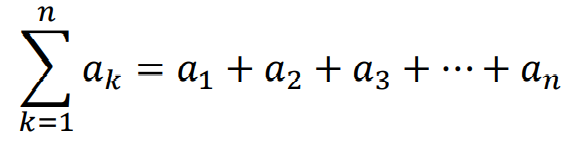

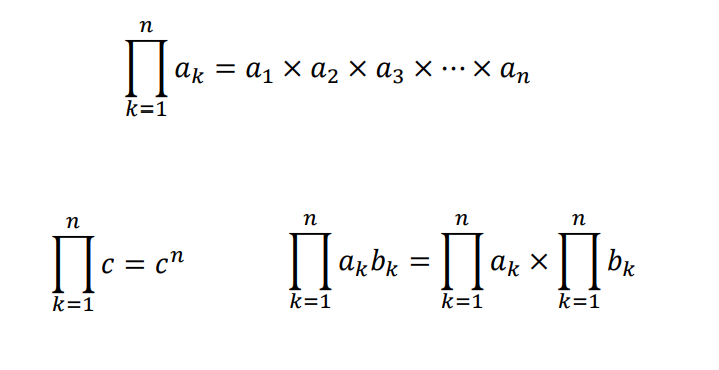
Comments powered by Disqus.