[이산수학] 집합과 논리

이번 시간에는 인공지능을 위한 기초수학 중에서 이산수학에 대해서 알아보려고 합니다.

이산 = discrete, 즉 별개의, 개별적인, 분리된 이런 뜻인데요.

이런 이산적인 수학 구조를 연구하는 학문이고 인공지능에서 쓰인다고 하네요!

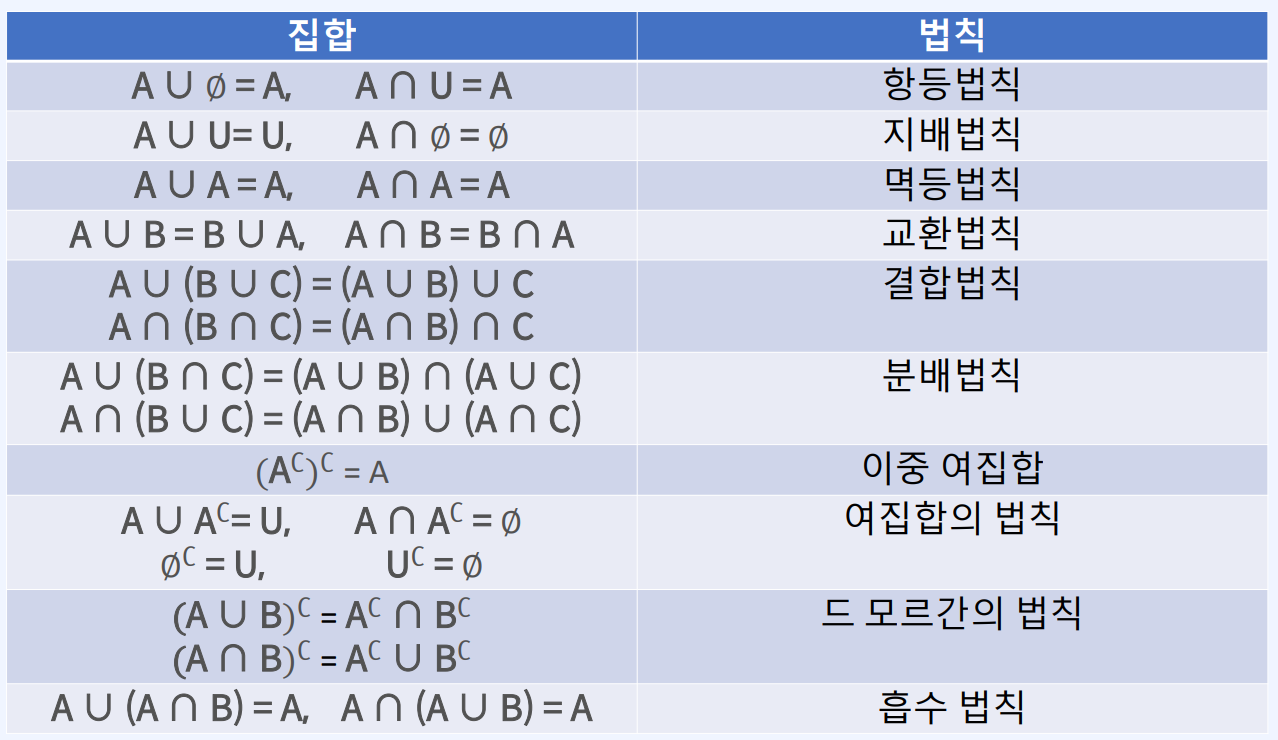
집합

여러 원소들(element)의 모임으로 중복된 원소를 가지지 않습니다.

유한집합/무한집합

집합 A에 속하는 원소의 개수를

A

로 표현하며, 원소가 유한개인 집합을 유한집합, 원소가 무한개인 집합을 무한집합이라고 합니다.

사실 고등학교 때부터 배워온 거라 집합에 대해 전부 다루진 않고 필요한 것들만 올릴게요!

명제

객관적으로 참, 거짓을 판단할 수 있는 문장이나 수식. 이때, 보통 참인 경우 알파벳 T로 거짓인 경우 알파벳 F로 표시한다. 참, 거짓을 가리키는 값을 진릿값(Truth value)라고 합니다.

다음 중 명제는 무엇일까?

1. 신동희는 잘 생겼다.

2. 신동희는 머리가 좋다.

3. 신동희는 만 21살이다.

4. 1 + 1 = 2

어그로 끌어봤습니다. 1,2 번은 지극히 주관적인 영역이므로 명제라 할 수 없고, 3번은 명제지만 거짓인 명제, 4번은 참인 명제입니다.

논리

논리연산자들

부정 ~p

명제 p에 대하여 p의 진릿값을 반대로 갖는 명제를 위와 같이 표기하며 p가 아니다 또는 not p라고 읽는다. 참고: p가 참인 명제일 경우 ~p는 거짓, p가 거짓인 명제일 경우 ~p는 참입니다.

논리곱(and):

p ∧ q 명제 p, q에 대하여 p와 q가 모두 참일 경우에만 참이고, 그렇지 않을 경우 거짓이 되는 명제

논리합(or):

p ∨ q 명제 p, q에 대하여 p와 q가 모두 거짓일 경우에만 거짓이고, 그렇지 않을 경우 참이 되는 명제

조건 명제

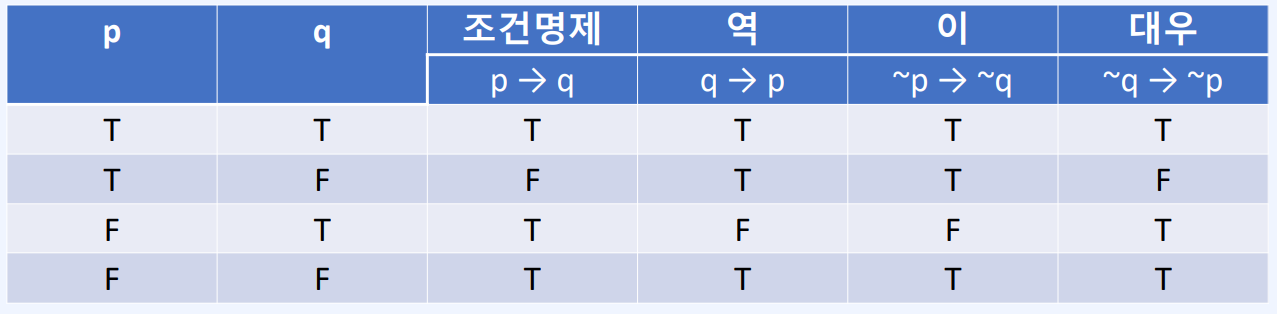
p → q 명제 p, q에 대하여 p가 가정이고 q가 결론이 되는 명제입니다. 이 때 p이면 q이다 또는 if p, then q 등으로 읽습니다.

역

조건 명제 p → q에 대하여 가정과 결론이 바뀐 q → p를 p → q의 역이라 부릅니다.

이

조건 명제 p → q에 대하여 가정과 결론을 각각 부정한 ~p → ~q를 p → q의 이라 부릅니다.

대우

조건 명제 p → q에 대하여 가정과 결론이 바뀐 동시에 부정한 ~q → ~p를 p → q의 대우라 부릅니다.

이번 시간엔 여기까지 하겠습니다! 오랜만에 옛날로 돌아간 것 같아서 기쁘네요 ㅎㅎ