[이산수학] 데이터 정리와 확률
이번 시간에는 데이터 정리와 확률에 대해서 인공지능에 접근해보겠습니다!
평균mean
데이터를 모두 더한 후 갯수로 나누 대푯값이며 가장 많이 사용되고 이상치에 민감하다는 특징이 있습니다.
중앙값median
데이터를 크기 순서로 나열한 후 가장 가운데 있는 값
분산variance
평균으로부터 퍼짐의 정도를 숫자로 표현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
np.random.seed(0)
scores1 = np.random.randint(30, 100, 10)
scores2 = np.random.randint(50, 90, 10)
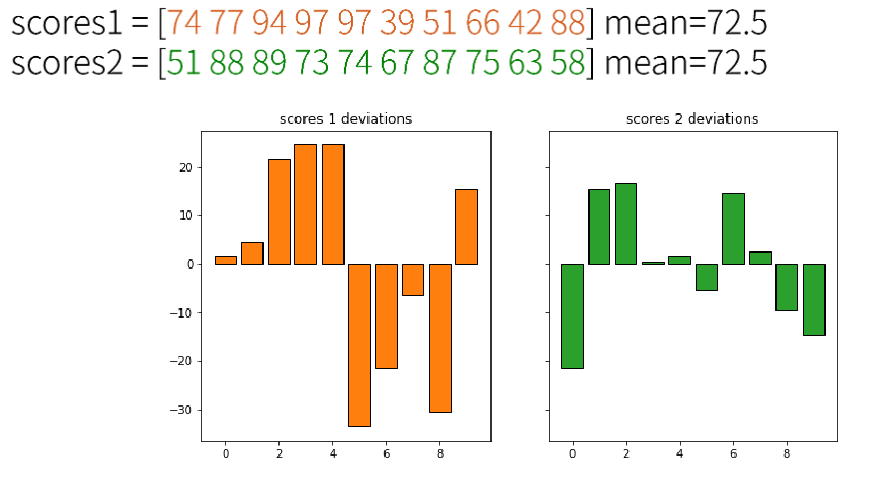
#scores1과 2는 평균이 같다
deviations1 = scores1 - scores1.mean()
deviations2 = scores2 - scores2.mean()
fig, ax = plt.subplots(figsize=(10,5), nrows=1, ncols=2, sharey=True)
ax[0].bar(np.arange(10), deviations1, color='C1', edgecolor='k')
ax[0].set_title('scores 1 deviations')
ax[1].bar(np.arange(10), deviations2, color='C2', edgecolor='k')
ax[1].set_title('scores 2 deviations')
plt.show()
평균이 같은데도 분산은 다르게 나타날 수 있습니다.
1
2
3
# numpy 기능으로 분산 바로 구하기 [+]
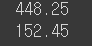
print(scores1.var())
print(scores2.var())
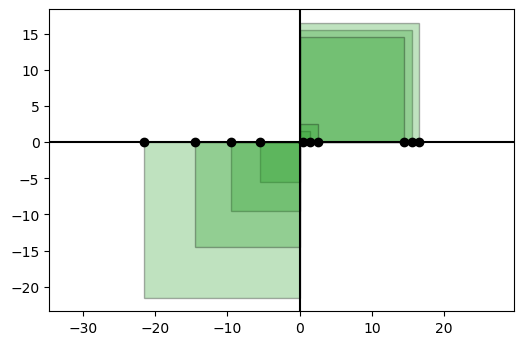
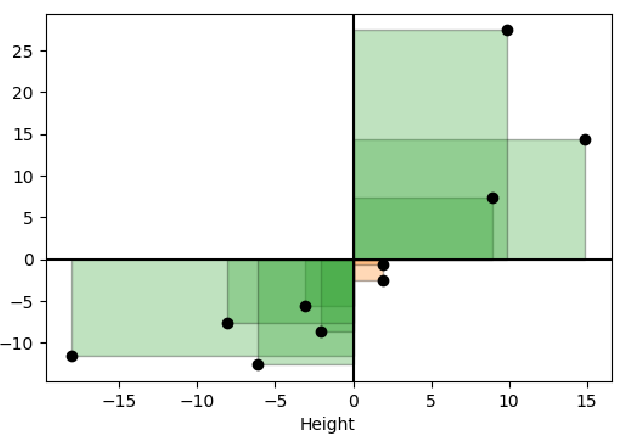
또한 분산은 평균으로부터 퍼짐의 정도를 한변으로 하는 사각형의 평균 넓이가 될 수 있습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from matplotlib.patches import Rectangle
fig = plt.figure(dpi=100)
ax = plt.axes()
# 0:- 1:+
colors = ['C1', 'C2']
covs = [ Rectangle( (0,0), x, x, edgecolor='k',
facecolor=colors[1], alpha=0.3)
for x in deviations2 ]
for cov in covs:
ax.add_patch(cov)
ax.plot(deviations2, np.zeros_like(deviations2), 'o', color='k')
ax.axhline(y=0, color='k')
ax.axvline(x=0, color='k')
ax.axis('equal')
plt.show()
이렇게 나타났을 때 사각형이 1,3분면에만 나타난 것을 보고 양의 상관관계까지 추론할 수 있겠죠?
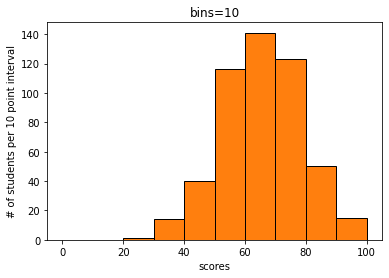
히스토그램
데이터를 계급으로 나눠 계급에 해당하는 빈도수를 막대그래프로 그린 그래프입니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
np.random.seed(0)
scores = np.abs((np.random.randn(500)*13)-65).astype(int)
scores[scores>=100] = 100
hist, bins = np.histogram(scores, bins=10, range=(0,100))
fig = plt.figure()
ax = plt.axes()
ax.hist(scores, bins=10, range=(0,100), color='C1', edgecolor='k')
ax.set_xlabel('scores')
ax.set_ylabel('# of students per 10 point interval')
ax.set_title('bins=10')
plt.show()
여기서 bins=를 더 크게주면 잘게 나눠지므로 그래프로 좀더 촘촘하게 나옵니다.
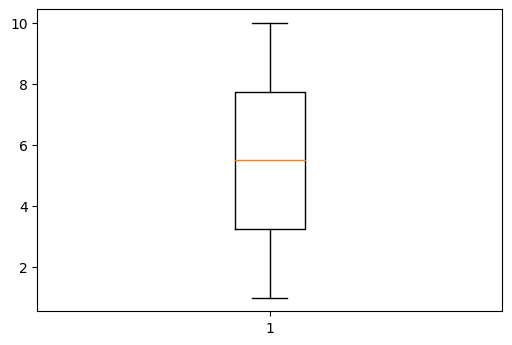
상자그래프 Boxplot
박스플롯은 전체 데이터에서 비율을 정해서 펜스를 min과 max각각 주어서 그것을 넘어가는 이상치를 구분할 수 있게 해줍니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
D = np.array([1,2,3,4,5,6,7,8,9,10])
Q1 = np.percentile(D, 25, interpolation='nearest') #interpolation: 옵션
Q2 = np.percentile(D, 50)
Q3 = np.percentile(D, 75, interpolation='nearest')
IQR = Q3 - Q1
upper_fence = Q3 + 1.5*IQR
upper_whisker = np.max(D[D<upper_fence])
lower_fence = Q1 - 1.5*IQR
upper_whisker = np.min(D[D>lower_fence])
fig = plt.figure(dpi=100)
ax = plt.axes()
ret = ax.boxplot(D)
plt.show()
n차원 데이터
n차원 데이터는 예를들어 키와 몸무게, 2차원으로 각각 열벡터로 표현한 하나의 행렬로써 표현할 수 있습니다.
공분산
두 평균으로부터 퍼짐의 정도를 한변으로 하는 사각형의 평균 넓이
양수: 두 데이터는 양의 직선관계, X증가 -> Y증가, X감소 -> Y감소,
음수: 두 데이터는 음의 직선관계, X증가 -> Y감소, X감소 -> Y증가,
거의 0: 직선의 관계가 없습니다.
주의 사항으로는 공분산이 크다고 관계가 더 강하거나 그런 것은 아닙니다. 왜냐하면 데이터의 수치( 몸무게를 그램으로 표기한다던가)가 크면 커지기 때문이죠.
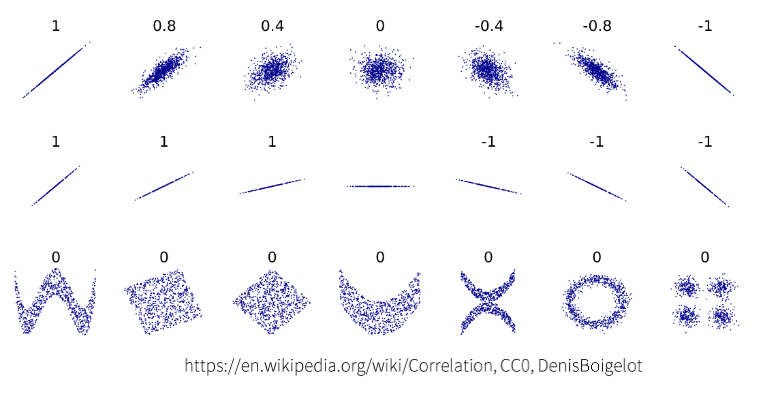
상관계수correlation coefficient
두 변수의 단위에 관계없이 상관성을 나타내는 지표
1에 가까우면: 두 데이터는 양의 상관관계, X증가 -> Y증가, X감소 -> Y감소
-1에 가까우면: 두 데이터는 음의 상관관계, X증가 -> Y감소, X감소 -> Y증가,
상관계수는 두 샘플 편차 벡터 사이각의 코사인 값이기 때문에 어떤 수를 넣어도 -1에서 1까지 표시됩니다. 시그모이드 함수와 비슷하죠.
순열
순열이란 서로 다른 n 개 중에서 m 개를 택하여 일렬로 배열하는 경우를 말합니다. 순서가 있기 때문에 (a,b)와 (b,a)는 다른 원소라 둘다 포함이 됩니다.
조합
순열에서 순서가 없는 버전이라고 생각하시면 편합니다. 즉 (a,b)와 (b,a)는 같은 원소이죠. 따라서 중복을 제거해야 정확한 값이 나옵니다.
조건부 확률
두 사건 A,B에 대해 A사건이 일어났을 때 사건 B가 일어날 확률이라고 보시면 됩니다. 따라서 A가 일어났다는 것을 조건으로 하는 확률입니다.
따라서 이런식이 나옵니다!
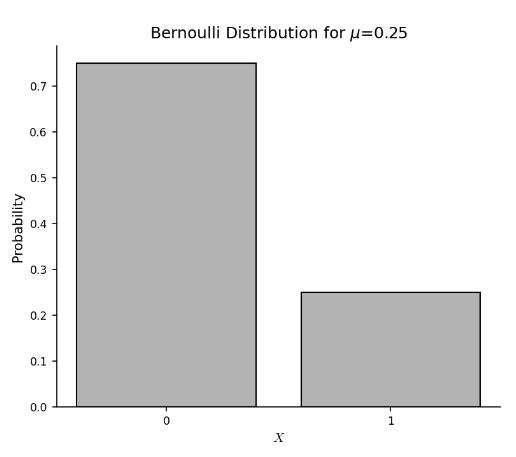
베르누이 분포Bernoulli distribution
0 또는 1을 값으로 가지는 바이너리 확률변수 X에 대한 분포.( 동전 던지기)
이것은 확률 질량함수에서 x=1일 확률을 mu=0.25로 두고 그린 분포그래프입니다.
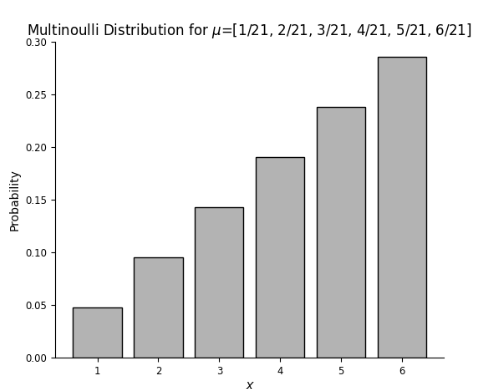
멀티누이 Multinoulli distribution
다항변수: 이진 변수의 일반화로 이진 변수가 여러 개가 모인 벡터 변수 X에 대한 확률분포(주사위 던지기)
제약조건으로는 각각의 변수의 모든 확률을 더한 값은 1이다.
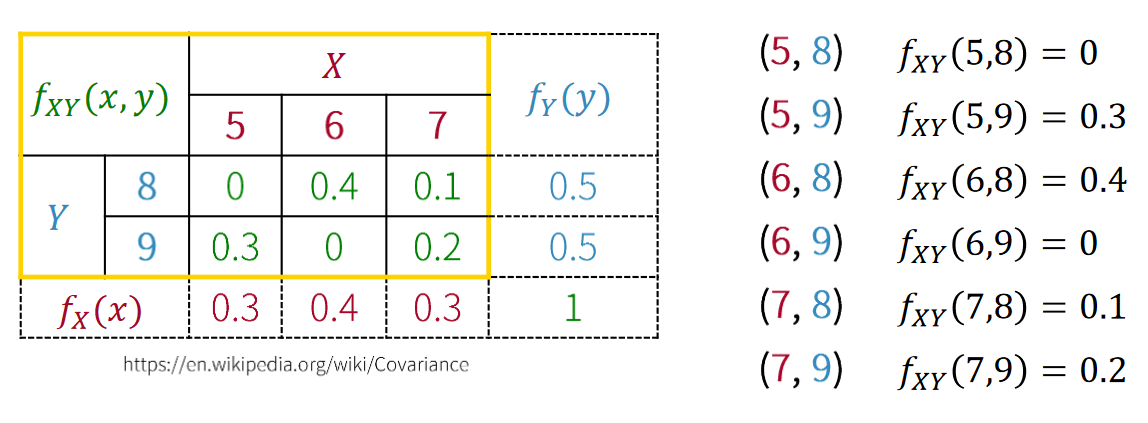
결합확률분포 joint probability distribution
이번 시간에는 여기까지 하겠습니다!
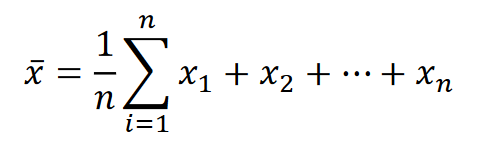

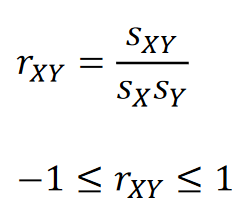

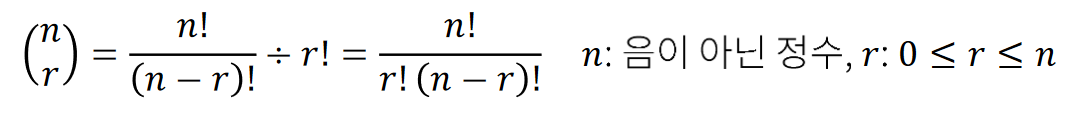
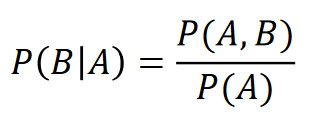
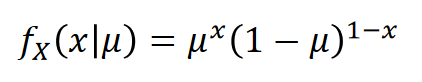
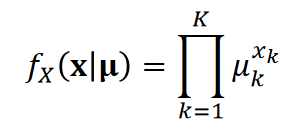
Comments powered by Disqus.