[이산수학] 행렬
이번 시간에는 행렬을 알아보겠습니다. 인공지능의 연산이 행렬연산으로 이루어지므로 유용하게 쓰입니다!
행렬?
사각 괄호로 둘러 쌓인 숫자들의 배열
이런식으로 나타내죠!
행렬의 연산은 다 아실테지만 곱셈은 중요하니 다뤄볼게요!
말 그대로 행과 열의 인덱스를 각각 곱해서 더한값을 하나의 원소로 결과가 나옵니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# 행렬과 행렬의 덧셈은 요소끼리 덧셈
A = np.matrix([[1,2],[3,4]])
B = np.matrix([[10,20],[30,40]])
A+B
# 행렬과 행렬의 곱셈
A = np.array([[1,2,3], [4,5,6]])
B = np.array([[2,1], [1,2], [1,1]])
print(np.dot(A,B)) #벡터의 곱하기
# 그냥 곱하면 에러가 남
# A*B
print(A@B) #파이썬에서 지원하는 행렬곱 연산자
########################################
# 그냥 곱하고 싶으면?
A_ = np.matrix(A)
B_ = np.matrix(B)
A_*B_
행렬의 전치
행렬의 전치는 주어진 행렬의 행과 열을 뒤바꾼 구조입니다.
이렇게 말이죠!
단위 행렬
대각 성분이 모두 1인 정사각 행렬
대각행렬
대각 성분만 0이 아닌 성분을 가진 정사각 행렬
행렬은 이런식으로 데이터 테이블을 표현할 때 쓰기도 합니다. 한 개체의 데이터를 행으로, 특징들을 열 데이터로 표현하였습니다.
이번 시간엔 여기까지 하겠습니다!
This post is licensed under CC BY 4.0 by the author.
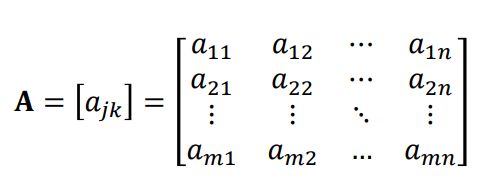
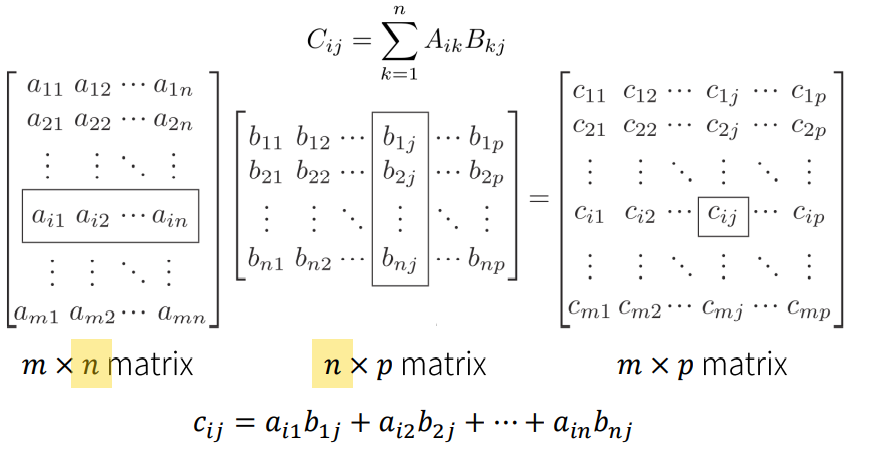
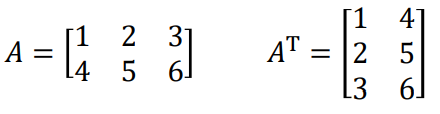
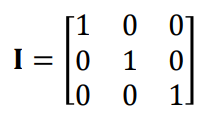
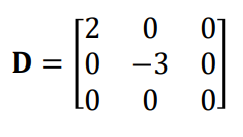

Comments powered by Disqus.