[이산수학] 알고리즘

이번 시간에는 IT분야의 꽃이라고 불리우는 알고리즘에 대해서 포스팅을 시작하려고 합니다! 다만 이산수학 카테고리니까 IT분야의 알고리즘 설명이 아닌 수학적 설명으로 접근해보겠습니다 ㅎㅎ

알고리즘?

주어진 문제에 대해 그 문제를 해결하기 위한 방법을 순차적으로 나열한 것입니다.

알고리즘의 특징

(1) 입력(input) : 입력값을 가집니다.

(2) 출력(output) : 출력값을 가집니다.

(3) 유한성(finiteness) : 유한 시간 내에 종료되어야 합니다.

(4) 정확성(precision) : 각각의 중간과정(step)은 명확하게 서술되어야 합니다.

(5) 일반성(generality) : 여러 입력값에 대해 적용 가능해야 합니다.

알고리즘의 표현 방법

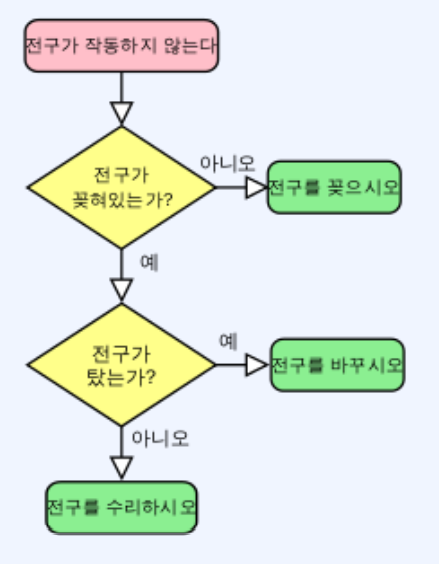
(1) 순서적인 도표를 사용해서 표현하는 순서도(flow chart)

(2) 실제적인 언어를 닮은 의사 코드(pseudo code)

(3) 실제 언어를 사용해서 표현하기

실제언어는 프로그래밍 언어부터 여러가지 종류가 있겠죠?

알고리즘의 분석 기준

(1) 정확도 (값이 얼마나 정확한가)

(2) 코드 복잡도 (코드가 인간이 보기에 얼마나 복잡하게 쓰여 있는가 등)

(3) 공간 복잡도 (RAM, 하드디스크 등의 하드웨어를 얼마나 사용하는가)

(4) 시간 복잡도 (주어진 입력자료에 대해 실행시간이 얼마나 긴 가)

정확도와 시간 복잡도가 주로 알고리즘에서 제일 중요한 요소로 여겨지는데, 정확도의 경우에는 문제에 따라 완전히 정확한 참값을 구해야 하는 문제가 있고 근삿값을 구해도 충분한 문제도 있는 등 경우에 따라 다르므로 이 챕터에서는 시간 복잡도 위주로 다루도록 하겠습니다.

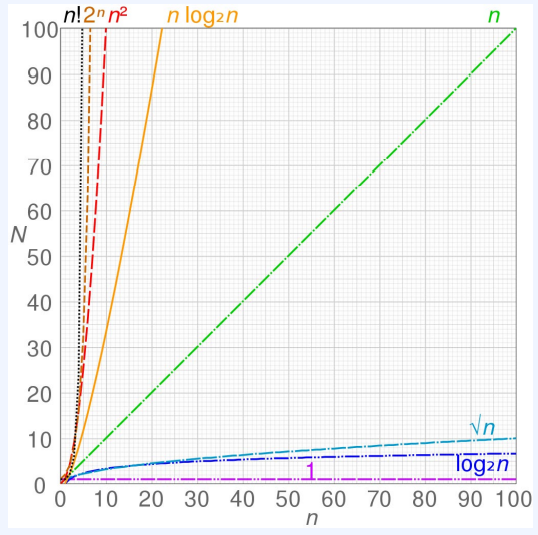
시간 복잡도 표기법

두 양의 정수 c와 𝑛0가 존재하여 𝑛 ≧ 𝑛0인 모든 n에서

f(𝑛)

≦ c

g(𝑛)

를 만족하면, f(n) = O(g(𝑛))이라고 쓰고, f(𝑛)은 Big-오 of g(𝑛) 또는 줄여서 오 g(𝑛)이다 라고 읽습니다. 이러한 표기법을 빅-오 표기법(notation)이라고 부릅니다.

이 때, 일반적으로 g(𝑛)에 들어가는 함수는 1, log 𝑛, 𝑛, 𝑛 log 𝑛,𝑛2 , 𝑛3 , 𝑛! 등이 있다고 하네요..

그냥 정보처리기사 책에서 보는 빅오 설명이랑 많이 다르죠? ㅎㅎ; 괜히 어렵게 쓴거같은데 수학에서는 어느하나 당연한 것이 없고 모든 것이 확실하게 구조되어야 하기 때문에 정확한 설명을 위해 이렇게 쓴 것 같습니다. 

추가적으로 여기서 말하는 함수에선 n이 충분히 클 때입니다!

재귀적 알고리즘

재귀적 함수란 함수가 자기 자신을 스스로 호출하는 함수를 말합니다. 재귀적 알고리즘이란 재귀적 함수를 포함한 알고리즘을 말합니다.

예시) f(n) = nf(n-1)으로 정의된 함수가 대표적인 재귀적 함수입니다.

f(n) = n(n-1)(n-2)…2‧f(1) = n!f(1) 입니다.

보통 위와 같이 재귀적인 문제를 해결하기 위해서는 초기 조건(initial condition, 위의 경우 f(1)의 값)과 재귀 조건(recursion condition)이 필요합니다.

일반적으로 재귀법은 반복법보다 프로그램의 구성이 간단하지만 실행시간이나 메모리를 더 많이 사용하는 단점이 있습니다. 대부분의 경우 재귀법을 사용한 프로그램과 반복법을 사용한 프로그램 사이에는 동등한 대체법이 존재할 수 있습니다.

이번 시간에는 여기까지 하겠습니다!