[이산수학] 함수2
이번 시간에는 함수를 다뤄보겠습니다. 기본적인 내용도 있고 인공지능에 어떻게 활용되는지도 다뤄볼게요!
함수란?
입력되는 변수와 출력되는 변수가 있을 때, 입력되는 변수가 어떤 형태로든 연산이 되어출력변수로 나오게 되는 구조.
첫 번째 집합의 임의의 한 원소를 두 번째 집합의 오직 한 원소에 대응시키는 대응관계
표기
표기 에제
단항식
2,x,x**2, x/3 등 상수 또는 변수의 항 하나로 이루어진 식
다항식
단항식 여러 개의 더하기로 연결된 식 3*x**2+2
다항함수
다항식으로 구성된 함수
f(x) = x**2+ 2*x +3
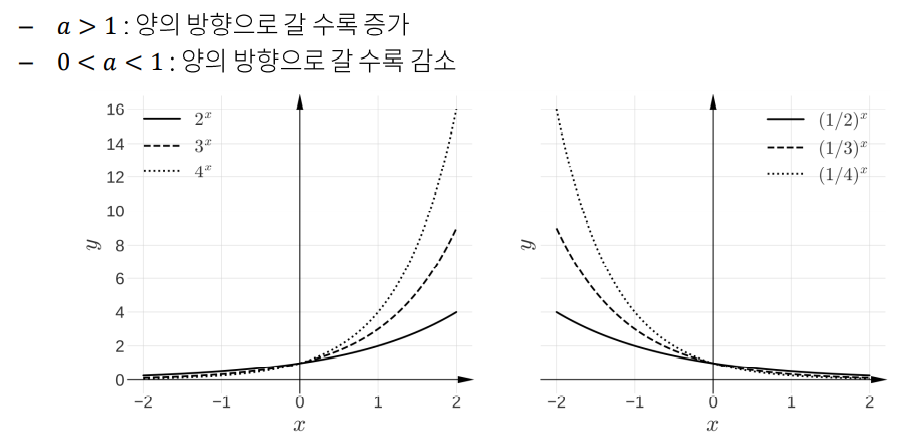
지수 함수
-0보다 큰 a라는 수의 지수가 변수인 함수
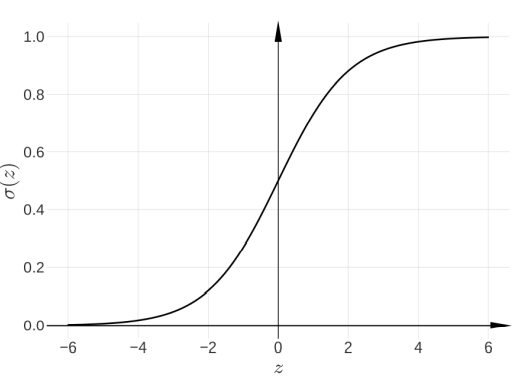
로지스틱 시그모이드 함수
신경망에서 뉴런의 활성을 결정하는 활성함수로 사용됩니다.
이 z에 어떤 실수를 넣어도 0~1사이로 값이 나와서 출력을 확률로 해석할 수 있습니다.
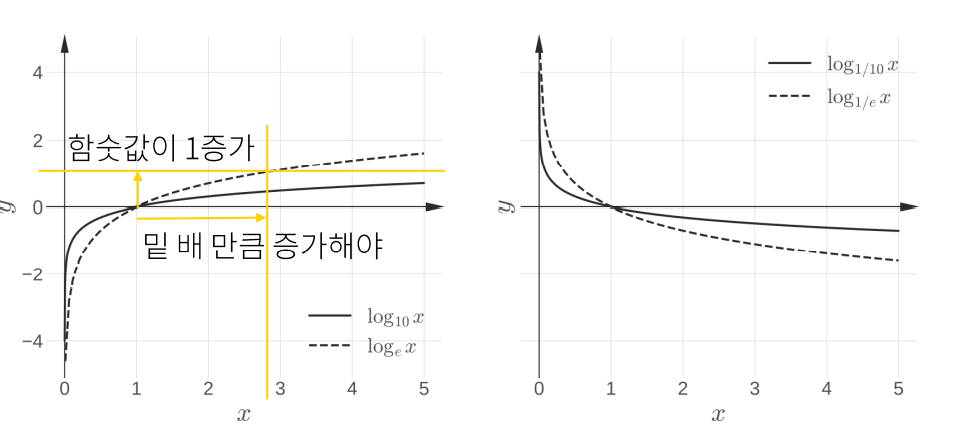
로그함수
로그함수는 지수함수의 y=x 에 대칭된 함수라고 할 수 있습니다
로그의 활용
예측값과 정답 사이에 예측률을 그냥 차이에서 제곱하는 것보다 더 정확하게 에러율을 나타낼 수 있습니다.
예를 들어, (예측값 - 정답)을 제곱해서 에러율을 표현하고자하면 10과 15, 그리고 1000과 1005가 같은 예측률을 보여주죠 하지만 10과 15는 엄청난 차이죠. 무려 50퍼센트입니다. 하지만 1000과 1005는 그렇게 큰 차이는 아니죠. 그런데 위식을 대입하면 둘다 25로 나옵니다. 그래서 로그를 붙여서 좀더 정확하게 알 수 있죠!
또한 로그는 중첩된 미분이 필요한 경우에 로그를 붙여서 간단하게 계산을 할 수 있습니다.
스칼라와 벡터
스칼라
스칼라 (수학): 벡터 공간에서 벡터를 곱할 수 있는 양 · 스칼라 (물리): 특정 좌표계와 관련이 없는 양 · 변수 (컴퓨터 과학): 한번에 하나의 값만 보유할 수 있는 원자량입니다.
벡터
양과 방향으로 표현할 수 있는 물리량, 공간의 두점 또는 원점과 한 점으로 정의
속도, 힘
숫자 여러 개
입력과 출력의 형태에 따른 분류
여기서 몇 가지 살펴봅시다.
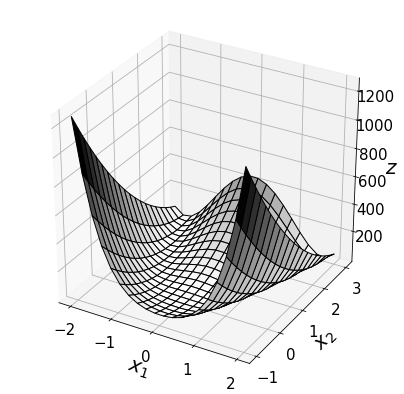
다변수 스칼라함수의 그래프
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import numpy as np
import matplotlib.pyplot as plt
from ipywidgets import interact
import ipywidgets as widgets
@interact( x=widgets.IntSlider(min=2, max=20, step=1, value=2) )
def draw_func(x):
fig = plt.figure(figsize=(7,7))
ax = plt.axes(projection='3d')
ax.xaxis.set_tick_params(labelsize=15)
ax.yaxis.set_tick_params(labelsize=15)
ax.zaxis.set_tick_params(labelsize=15)
ax.set_xlabel(r'$x_1$', fontsize=20)
ax.set_ylabel(r'$x_2$', fontsize=20)
ax.set_zlabel(r'$z$', fontsize=20)
x1 = np.linspace(-2, 2, x)
x2 = np.linspace(-1, 3, x)
X1, X2 = np.meshgrid(x1, x2)
Z = 50*(X2 - X1**2)**2 + (2-X1)**2
# ax.scatter3D(X1, X2, Z, marker='.', color='C1')
ax.plot_surface(X1, X2, Z, cmap=plt.cm.binary, edgecolor="k")
plt.show()
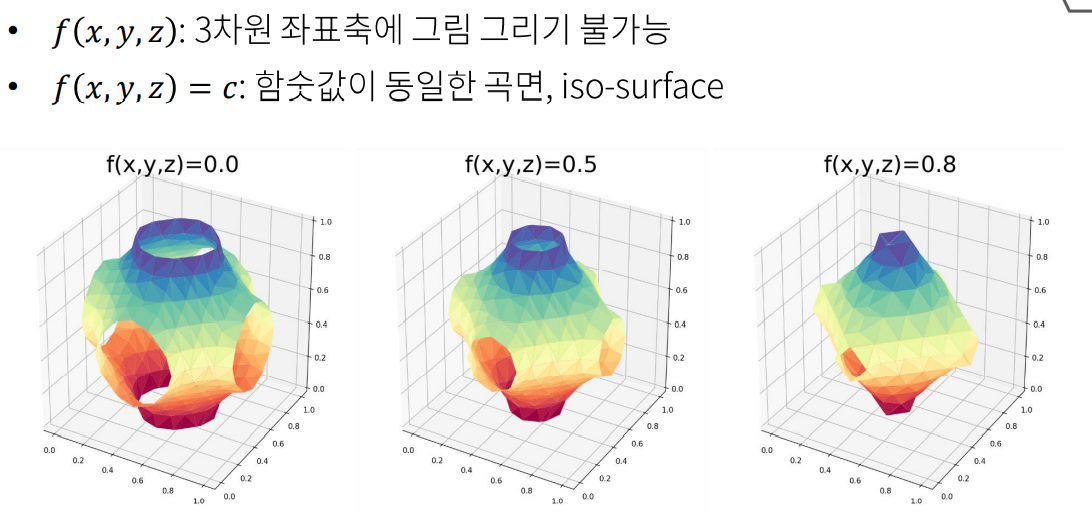
numpy와 matplotlib로 다변수 - 스칼라 함수 그래프를 표현합니다. 중요한 것은 변수가 2개일 땐 상수 c가 정해져 있다면 x,y에 대한 등고선의 그래프를 얻을 수 있고 변수가 3개라면 x,y,z에 대한 등고면을 얻을 수 있습니다. 변수가 3개일 때 상수까지 포함하는 것은 4차원이기 때문에 표현할 수 없습니다.
이번 시간에는 여기까지 하겠습니다!


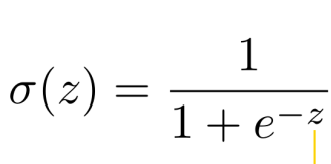


Comments powered by Disqus.