[이산수학] 함수 수열 관계

이번 시간엔 수학의 꽃인 함수와 수열 그리고 관계에 대해서 알아보겠습니다!

함수( f: A → B)

집합 A, B에 대하여 모든 집합 A의 원소에 대하여 집합 B의 원소가 하나씩 대응될 때, 그 대응 관계를 나타내는 것을 함수 f: A → B 라고 쓰고 A에서 B로 가는 함수 f라고 읽습니다. 또한, A의 원소 a에 대해 a에 대응되는 b의 값을 f(a)라고 씁니다. 중요한건 A에서 각 원소는 한번만 대응해야합니다. 두 갈래로 나가선 안 된다는 말이죠.

함수 f: A → B 가 있다고 하면

정의역 : f가 정의된 집합 A를 f의 정의역 이라고 합니다.

공역 : B를 f의 공역이라고 합니다.

치역 : {b

∃ a ∈ A such that f(a) = b} 즉, 치역은 B의 원소 중에서 f로 인해 A의 원소와 대응되는 것들의 모임입니다.

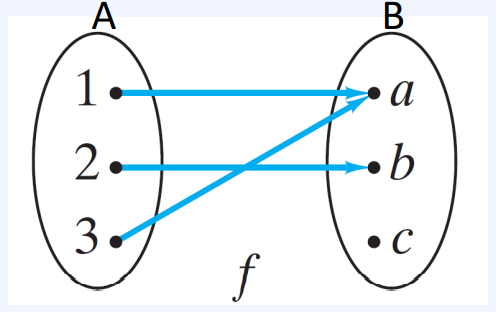
위의 사진에선 정의역은 {1, 2, 3}이고 공역은 {a, b, c}이며 치역은 {a, b}이겠죠.

일대일 함수(단사 함수)

정의역이 모든 원소들이 서로 다른 공역의 원소와 대응 하는 함수.

전사함수

공역과 치역이 일치하는 함수

일대일 대응함수(전단사함수)

일대일 함수 중에서 공역과 치역이 일치하는 함수.

합성함수

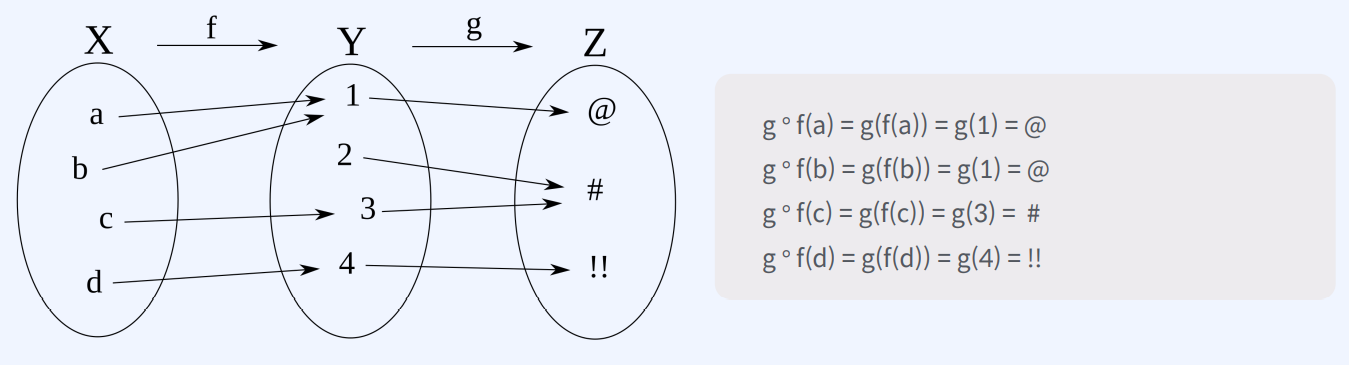
두 함수 f: A → B, g: B → C 에 대하여 두 함수를 연속적으로 적용한 함수를 g ° f: A → C 로 쓰며 A의 원소 a에 대하여 g ° f(a) = g(f(a))입니다.

합성함수의 특성

집합 A, B, C에 대하여 f: A → B, g: B → C이고 g ° f: A → C가 합성함수라고 하면

이 때, 다음과 같은 성질들이 성립합니다.

(1)f와 g가 일대일 함수면 g ° f도 일대일 함수입니다.

(2)f와 g가 전사함수면 g ° f도 전사함수입니다.

(3)f와 g가 일대일 대응 함수면 g ° f도 일대일 대응 함수입니다.

(4) g ° f가 일대일 함수이면 f도 일대일함수입니다.

(5) g ° f가 전사함수이면 g도 전사함수입니다.

(6) g ° f가 일대일 대응 함수이면 f는 일대일함수이고 g는 전사함수입니다.

각 특성은 벤다이어그램으로 증명 및 확인할 수 있습니다.

수열

함수 중에서 정의역이 자연수의 부분집합인 함수를 수열이라 합니다.

이 때, 자연수는 크기순서로 나열할 수 있으므로 편의상 정의역은 {1, 2, 3, … }라고 하면,

자연수에서 정의된 수열 s에 대하여 s(n)을 편의상 s𝑛라고 적고 n을 s의 index라고 합니다.

이때 편의상, s: A → B 라는 표현 대신 {s𝑛}𝑛 ∈ 𝐴 로 표기합니다.

정의역이 유한 집합인 수열을 유한수열, 정의역이 무한집합인 수열을 무한수열이라 합니다.

이렇게 수학적인 표현으로 보니까 어려워보이는데 사실 그렇게 어려운 것도 아닙니다. 우리가 알고 있는 등차수열,등비수열, 피보나치수열 등등.. 여기에 해당하는 것입니다.

수열 {s𝑛}𝑛 ∈ 𝐴 가 있다고 하면,

이 때, 어떤 부분집합 B ⊂ A가 존재하여 index의 크기순서를 유지한 {s𝑛}𝑛 ∈𝐵를 {s𝑛}𝑛𝑛 ∈ 𝐴 의 부분수열이라 합니다.

관계

순서쌍

어떤 원소 a ∈ A, b ∈ B에 대하여 (a, b)와 같이 순서를 가진 쌍을 순서쌍이라 하며 a를 첫 번째 원소, b를 두 번째 원소라고 합니다.

곱집합(cartesian product)

공집합이 아닌 임의의 두 집합 A, B에 대해 a ∈ A, b ∈ B인 모든 순서쌍 (a, b)를 모아놓은 집합을 A와 B의 곱집합이라 하며 A × B로 표기합니다. A × B = {(a, b)

a ∈ A, b ∈ B}

곱집합의 크기

유한집합 A, B에 대해

A × B

=

A

×

B

입니다.

이항 관계 ( binary relation )

집합 A, B에 대하여 A에서 B로 가는 관계 R은 A × B의 부분집합으로 정의됩니다. 이 때, (a, b) ∈ R이면 a는 b에 대하여 R의 관계에 있다고 하며 a R b 로 표시합니다.

함수와 관계

함수 f는 관계의 특수한 형태입니다. f의 정의역이 A 전체이고 a ∈ A에 대하여 a R b를 만족하는 b ∈ B가 단 하나만 존재하는 관계를 함수라고 합니다.

관계의 표현

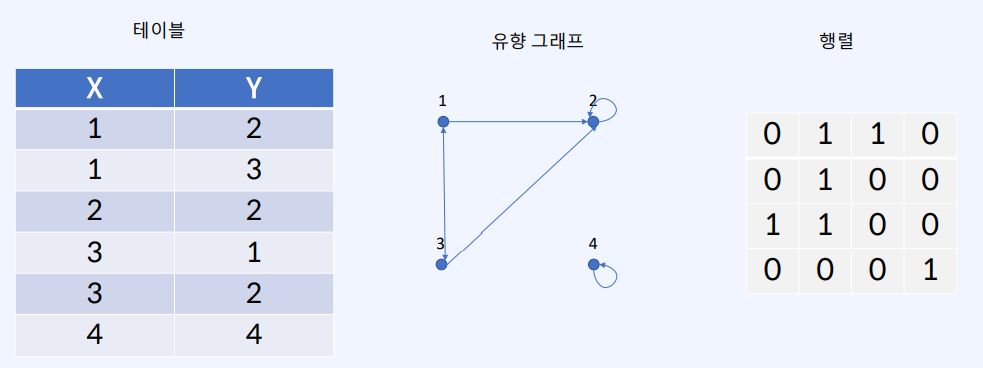
X = {1, 2, 3, 4} 이라 하자. X × X 에서 정의된 관계 R이 있다고 하면, R = {(1, 2), (1, 3), (2, 2), (3, 1), (3, 2), (4, 4)} 일 때, 다음과 같은 표현법들이 가능합니다.

X × X 에서 정의된 관계 R이 있다고 하면,

(1) 모든 원소 x ∈ X에 대해 (x, x) ∈ R이 성립하면 반사(reflexive) 관계라 합니다.

(2) 모든 순서쌍 (x, y) ∈ R에 대해 (y, x) ∈ R도 성립한다면 대칭(symmetric)관계라 합니다.

(3) 모든 순서쌍 (x, y) ∈ R에 x, y가 서로 다를 경우 (y, x) ∉ R 가 성립하면 반대칭(antisymmetric) 관계라 합니다.

(4) (x, y) ∈ R, (y, z) ∈ R 가 성립하는 모든 x, y, z ∈ R에 대해 (x, z) ∈ R도 만족한다면 추이(transitive) 관계라 합니다.

이번 시간에는 함수와 수열과 관계에 대해서 알아봤습니다~